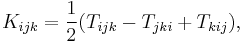Contorsion tensor

The contorsion tensor in differential geometry expresses the difference between a metric-compatible affine connection with Christoffel symbol 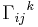$\Gamma_{ij}{}^k$ and the unique torsion-free Levi-Civita connection for the same metric.

The contortion tensor 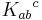${K_{ab}}^c$ is defined in terms of the torsion tensor 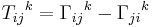${T_{ij}}^k= {\Gamma_{ij}}^k -{\Gamma_{ji}}^k$ as

$K_{ijk}= \frac{1}{2} (T_{ijk} - T_{jki} %2B T_{kij} ),$

where the indices are being raised and lowered with respect to the metric:

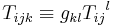$T_{ijk} \equiv g_{kl} {T_{ij}}^l$ .

The reason for the non-obvious sum in the definition is that the contortion tensor, being the difference between two metric-compatible Christoffel symbols, must be antisymmetric in the last two indices, whilst the torsion tensor itself is antisymmetric in its first two indices.

The connection can now be written as

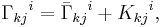
${\Gamma_{kj}}^i =\bar\Gamma_{kj}{}^i %2B {K_{kj}}^i,$

where 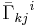$\bar\Gamma_{kj}{}^i$ is the torsion-free Levi-Civita connection.